Convex madness 01

Aim of this issue is to straight out our goals and then design a simple polygon class and try some nice code to get it drawn under OpenGL.
One more thing before we get started ... i may sometimes presume knowledge of something. Don't get scared, just google it or look into wikipedia. That should do it ...
As (i suppose) everyone knows, polygon is geometrical shape, given by n vertices (where n > 2), connected by it's edges. Edges then enclose interior of polygon. It's good thing to point out all polygons we will be working with will be planar (that means all vertices of every individual polygon will lie in the single plane) and as name of series suggests, all polygons we will be working with will be convex. Convex polygon is polygon with all interior angles (angles held by it's edges, meassured over polygon's interior) below or equal to 180 degrees (or Pi radians)
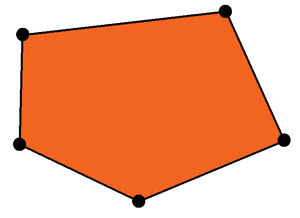
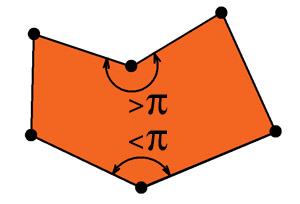
(on the left is convex polygon, on the right is concave polygon with two interior angles marked)
FPU curse
There is one thing that one should keep on his mind when working with computer graphics. Precission of floating point arithmetics (which is used in today's computers) is not infinite. It brings us some trouble as two numbers can be very close but not equal. For example:
float a = .3f, b = .4f, c = .5f;
float c2 = (float)sqrt(a * a + b * b);
if(c == c2)
printf("the triangle is perpendicular\n");
else
printf("the triangle is not perpendicular\n");
This code snippet should decide wheter triangle ABC is perpendicular. It can be proven by checking Pythagoras' theorem. It says something like c = sqrt(a2 + b2). You can see the triangle with sides in ratio 3:4:5 should be perpendicular, but the code snippet would decide opposite. Why is that? That's because result in c2 will not be .5 but instead something like .49999... Unfortunately when you try to print the numbers using any standard library function (or see them in your debugger) they will propably both be displayed as .5. That can be sometimes very frustrating as it's rather hard to understand why .5 is not equal to .5. Fortunately in cases simple like this it's easy to fix it with epsilon.
Epsilon is a greek alphabet letter and is used to denote the precission. So how should we proceed? It could be like this:
const float f_epsilon = 1e-3f;
float a = .3f, b = .4f, c = .5f;
float c2 = (float)sqrt(a * a + b * b);
if((float)fabs(c - c2) < f_epsilon)
printf("the triangle is perpendicular\n");
else
printf("the triangle is not perpendicular\n");
So what does this do? This subtracts numbers to be compared and see if the result is small enough to say the numbers are equal. This will be the same with everything. Distance of points in space, distance of point to plane in space, etc. The major drawback of this is that in case you deal with numbers, comparable with epsilon it will consider too much numbers to be equal. Sometimes it's enough to have more different epsilons for different kinds of values, but sometimes you just need to find more clever sollution to workaround your problem. And that's the hard part. I'll point out some common sollutions to some common problems later on.
This is not the only issue of floating point numbers. Next one could be limited number of represented decimal places. 32-bit floating point number (float type in C/C++ languages) is precise to about five decimal places. What is so bad about it? Consider two numbers, one million and one. Adding them up would yield one million again. Why? Because the one would be on sixth decimal place and therefore is cut off. It's not so bad error you say, only about 10-4%. But what about adding one to million, million times. The result should be two millions but it won't be ... and that's 100% error. It's therefore necessary to think about possible values your algorithms will have to cope with and order the operations in such a manner the chance for two incommensurate numbers to meet is minimal. (this applies to adding or subtracting only, multiplying and dividing isn't affected like this)
T-Junctions
Speaking of errors and artifacts, it's good to mention T-junctions as it's offen forgotten topic. T-junction is situation when adjoining edges don't share all vertices (T-junction is where long edge adjoins two shorter edges sharing vertex in the centre of long edge, hence the name)
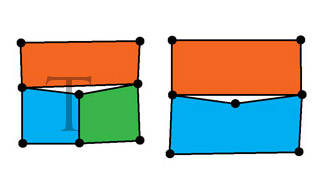
The image above contains the classical T-junction on the left (edges shared by polygons look like "T" letter) and a similar situation on the right. Both situations can be solved by adding vertex in the centre to orange polygon as well (on the following image). Such a process is called T-junction removal.
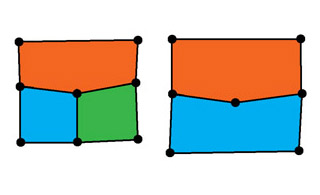
Note someone could point out the blue polygon on right half of image is not convex and he'd be right, but. But the center vertex is exaggertedly shift away from the orange polygon edge just to better illustrate the problem, and again - our arithmetics is finite-precision so even in case it's a little concave, we say it contains edges holding angle near to Pi radians and is convex.
Writing reusable and flexible polygon class
Now to start with our polygons. We are writing polygon class in C++. What do we expect? It's good to have polygon class made as template with vertex class parameter. Why? Because it's more reusable then. Sometimes, we have polygons where vertices hold their bare positions, sometimes (in computer graphics offen) vertices can hold more coordinates such as texture coordinates, vertex colors, normals, etc.
Should be vertices in a global container or should every polygon hold it's own list of vertices? As i'll show you, it's very simple to acheive both with the single class with actually verry little effort. For sake of clarity, it's practical to use polygons with their own (private) vertex lists in case those polygons aren't supposed to be somehow connected or in case there is very little of them. It's generaly simpler and faster solution. (because vertices can be in a single block of memory. to the contrary in case there is global vertex list, each polygon would hold list of indices or pointers which will require one more memory access) On the other hand, in case polygons form some real-world object or even building, it's practical to have global vertex list because polygons with adjoining edges should share vertices to avoid rasterization aretifacts when displaying them. (they manifest themselves as hair-thin gaps between polygons; it saves some memory as well)
The ultimate pro for global vertex list is rendering speed. We would have some vertex buffer containing vertex coordinates, located in our graphics card fast memory and then some index buffer containing polygon vertex indices (which could be in grahics card memory as well or could be transferred via graphics bus as indices will require far less bandwidth than vertices would) We are then able to draw lots of polygons using a few commands (essentialy we just say draw polygon using those indices, draw another one, next one, etc ... we will get to it on the end of this issue)
So ... to start coding. Our first polygon class:
template <class TVertStruct>
class CPolygon2 {
protected:
std::vector<TVertStruct> m_vertex_list;
Plane3f m_t_normal;
public:
// ...
};
We have quite simple template class, containing vector of vertices and normal plane (that is plane polygon lies on) It would be good to add some operators to add, delete and access vertices:
/*
* void Delete()
* - delete all polygon vertices
*/
void Delete()
{
m_vertex_list.clear();
}
/*
* inline bool Add_Vertex(const TVertStruct &r_t_vertex)
* - add single vertex past the last vertex in the array
*/
inline bool Add_Vertex(const TVertStruct &r_t_vertex)
{
return Add_Vertex(0, &r_t_vertex, 1);
}
/*
* inline bool Add_Vertex(int n_insert_before, const TVertStruct &r_t_vertex)
* - add single vertex before the n_insert_before-th vertex in the array
*/
inline bool Add_Vertex(int n_insert_before, const TVertStruct &r_t_vertex)
{
return Add_Vertex(n_insert_before, &r_t_vertex, 1);
}
/*
* inline bool Add_Vertex(const TVertStruct *p_vertex, int n_count)
* - add array of vertices past the last vertex in the array
*/
inline bool Add_Vertex(const TVertStruct *p_vertex, int n_count)
{
return Add_Vertex(0, p_vertex, n_count);
}
/*
* bool Add_Vertex(int n_insert_before, const TVertStruct *p_vertex, int n_count)
* - add array of vertices before the n_insert_before-th vertex in the array
*/
bool Add_Vertex(int n_insert_before, const TVertStruct *p_vertex, int n_count)
{
_ASSERTE(n_count > 0);
_ASSERTE(n_insert_before >= 0 && n_insert_before <= m_vertex_list.size());
m_vertex_list.reserve(m_vertex_list.size() + n_count);
if(m_vertex_list.capacity() < m_vertex_list.size() + n_count)
return false;
m_vertex_list.insert(m_vertex_list.begin() + n_insert_before,
p_vertex, p_vertex + n_count);
return true;
}
/*
* void Delete_Vertices(int n_index, int n_count)
* - delete n_count vertices, beggining with vertex n_index
*/
void Delete_Vertices(int n_index, int n_count)
{
m_vertex_list.erase(&m_vertex_list[n_index], &m_vertex_list[n_index + n_count]);
}
/*
* inline int n_Vertex_Num() const
* - return number of vertices
*/
inline int n_Vertex_Num() const
{
return m_vertex_list.size();
}
/*
* inline TVertStruct &r_t_Vertex(int n_index) const
* - vertex access function
* - doesn't check array bounds
*/
inline TVertStruct &r_t_Vertex(int n_index)
{
return m_vertex_list[n_index];
}
/*
* inline TVertStruct &t_Vertex(int n_index) const
* - vertex access function
* - doesn't check array bounds
*/
inline const TVertStruct &t_Vertex(int n_index) const
{
return m_vertex_list[n_index];
}
Now we can access vertices. That's great. But it would be more useful to define some simple operations with polygon, such as calculating it's center or it's normal plane. To do that, it's necessary to define interface TVertStruct classes should exhibit for use with this template. Basically we need to determine vertex position as it is essential for most operations and then some means to interpolate vertices. We could end up with something like this:
struct TMyVertex {
// member variables, some handy constructors ...
/*
* inline operator Vector3f() const
* - conversion to Vector3f should return vertex position
*/
inline operator Vector3f() const;
/*
* inline TMyVertex operator =(const Vector3f &r_v_position)
* - assigning Vector3f should write to vertex position
*/
inline TMyVertex operator =(const Vector3f &r_v_position);
/*
* inline TMyVertex operator =(const TMyVertex &r_t_vertex)
* - we need to specify such an assignment as well to avoid converting
* TMyVertex to Vector3f when assigning to another TMyVertex
*/
inline TMyVertex operator =(const TMyVertex &r_t_vertex);
/*
* inline bool operator ==(const TMyVertex &r_t_vertex)
* - we might need means to compare two vertices
* - constant f_epsilon is used as maximal coordinate distance tolerance
*/
inline bool operator ==(const TMyVertex &r_t_vertex);
/*
* TVertex operator *(float f_scalar) const
* - return vertex, scaled by f_scalar
*/
TMyVertex operator *(float f_scalar) const;
/*
* TMyVertex operator +(const TMyVertex &r_vertex) const
* - return vertex with sum of coordinates of both original vertices
*/
TMyVertex operator +(const TMyVertex &r_vertex) const;
/*
* TVertex operator *=(float f_scalar)
* - return vertex, scaled by f_scalar
*/
TMyVertex operator *=(float f_scalar);
/*
* TMyVertex operator +=(const TMyVertex &r_vertex)
* - return vertex with sum of coordinates of both original vertices
*/
TMyVertex operator +=(const TMyVertex &r_vertex);
};
This is quite useful because now we can have vertices with any coordinates and our polygon class should easily handle most of the basic operations. Now think about vertex class that would make it possible to use global vertex list. It would contain just pointer to simple vertex structure and all of the member functions described in code listening above. (so the implementation of global vertex list is complettely hidden from the polygon class)
It sounds simple, but unfortunately it's not so quite simple. Consider what happens when i want to add two vertices together. Vertex coordinates will be read from global vertex pool, will be added and new vertex is created. Now we need to put it into the pool. For that, vertices needs to know which pool they belong to. So now we have pointer to vertex structure in the pool and reference (or pointer) to the pool itself. It's a bit wasteful because each vertex will need to contain such an extra pointer (unless you can live with single vertex pool for all the vertices ever to be created and can make it static variable - which can be sometimes possible)
There is one more problem. Consider operation where we make several steps before we have our final vertex, for example calculating polygon centre. It would require several vertex add operations and then vertex scale operation (divide by vertex count to get average position, ie. polygon centre) In case vertex class behaved as described in the last paragraph, after every operation a new vertex would be inserted into vertex pool. We'd get awfuly lot of junk vertices. Sollution to this problem is simple, we need to have intermediate vertex type to carry out all operations which will then be converted to regular vertex type and during that conversion it will be added to the global vertex pool. It's easy and fast ... Here is how such a vertex class could look like:
struct TRefVertex {
TMyVertex *m_p_ref; // referenced vertex
std::vector<TMyVertex*> &m_r_vertex_pool;
// vertex pool (here we're going to add new vertices)
typedef TMyVertex TIntermediate;
// intermediate type for calculations will be TMyVertex
/*
* inline TRefVertex(const TMyVertex &r_t_vertex,
* std::vector<TMyVertex*> &r_vertex_pool)
* - default constructor
*/
inline TRefVertex(const TMyVertex &r_t_vertex, std::vector<TMyVertex*> &r_vertex_pool)
:m_p_ref(0), m_r_vertex_pool(r_vertex_pool)
{
m_p_ref = new TMyVertex(r_t_vertex); // alloc a new TMyVertex
m_r_vertex_pool.push_back(m_p_ref); // insert it to the list
}
/*
* inline TRefVertex(const TRefVertex &r_t_vertex)
* - copy constructor
*/
inline TRefVertex(const TRefVertex &r_t_vertex)
:m_p_ref(r_t_vertex.m_p_ref), m_r_vertex_pool(r_t_vertex.m_r_vertex_pool)
{}
/*
* inline TRefVertex operator =(const TRefVertex &r_t_vertex)
* - copy operator = (need it to avoid unwanted conversions)
*/
inline TRefVertex operator =(const TRefVertex &r_t_vertex)
{
m_p_ref = r_t_vertex.m_p_ref;
m_r_vertex_pool = r_t_vertex.m_r_vertex_pool;
return *this;
}
/*
* inline TRefVertex operator =(const TMyVertex &r_t_vertex)
* - conversion from TMyVertex to TRefVertex (conversion
* is solved by adding vertex to the vertex list)
*/
inline TRefVertex operator =(const TMyVertex &r_t_vertex)
{
m_p_ref = new TMyVertex(r_t_vertex); // alloc a new TMyVertex
m_r_vertex_pool.push_back(m_p_ref); // insert it to the list
return *this;
}
/*
* inline operator TMyVertex() const
* - now we need means to convert vertex type to intermediate vertex type
*/
inline operator TMyVertex() const
{
return *m_p_ref;
}
/*
* inline operator Vector3f() const
* - conversion to Vector3f should return vertex position
*/
inline operator Vector3f() const
{
return m_p_ref->v_position;
}
/*
* inline TRefVertex operator =(const Vector3f &r_v_position)
* - assigning Vector3f should write to vertex position
*/
inline TRefVertex operator =(const Vector3f &r_v_position)
{
m_p_ref->v_position = r_v_position;
return *this;
}
inline bool operator ==(const TMyVertex &r_t_vertex);
TMyVertex operator *(float f_scalar) const;
TMyVertex operator +(const TMyVertex &r_vertex) const;
// those just call TMyVertex functions for m_p_ref
TRefVertex operator *=(float f_scalar);
TRefVertex operator +=(const TMyVertex &r_vertex);
// those call TMyVertex functions for m_p_ref as well but
// returns TRefVertex because no new vertex originated
// (coordinates of some existing vertex were changed only)
};
This about sums it up. Now we need to think a little what we can do and what we can't do with this. We can interpolate vertex positions and with a little care vertices as well (we can't create TRefVertex out of nothing because our polygon class doesn't know anything about vertex pool which is necessary for TRefVertex constructor, but we can use TRefVertex copy-constructor and copy vertex pool address from another vertex that is already in the polygon; in some cases we just may return vertex intermediate type and let caller handle it)
Adding first operations
I'm going to add two functions for calculating polygon's centre (they're it's members) and some testing code so it's clear how such a polygon class can be used:
template <class TVertStruct>
class CPolygon2 {
protected:
std::vector<TVertStruct> m_vertex_list;
Plane3f m_t_normal;
public:
// we have already seen functions for vertex access
/*
* const Vector3f v_Center() const
* - return position of center of polygon
* - if polygon has no vertices, return the O vector
*/
const Vector3f v_Center() const
{
if(!m_vertex_list.size())
return Vector3f(0, 0, 0);
Vector3f v_center(0, 0, 0);
for(int i = 0; i < m_vertex_list.size(); ++ i)
v_center += m_vertex_list[i];
return v_center * (1.0f / m_vertex_list.size());
}
/*
* const TVertStruct::TIntermediate v_Center2() const
* - return vertex in center of polygon
* - if polygon has no vertices, return the O vertex
*/
const TVertStruct::TIntermediate v_Center2() const
{
TVertStruct::TIntermediate t_center(Vector3f(0, 0, 0));
if(!m_vertex_list.size())
return t_center;
for(int i = 0; i < m_vertex_list.size(); ++ i)
t_center += m_vertex_list[i];
return t_center * (1.0f / m_vertex_list.size());
}
};
int main()
{
{
CPolygon2<TMyVertex> t_my_polygon;
t_my_polygon.Add_Vertex(TMyVertex(-1, -1, 0));
t_my_polygon.Add_Vertex(TMyVertex( 1, -1, 0));
t_my_polygon.Add_Vertex(TMyVertex( 1, 1, 0));
t_my_polygon.Add_Vertex(TMyVertex(-1, 1, 0));
// add some vertices
Vector3f v_center = t_my_polygon.v_Center();
TMyVertex t_center = t_my_polygon.v_Center2();
// get center position and center vertex
}
// test with individual vertex list inside polygon
{
CPolygon2<TRefVertex> t_my_polygon;
std::vector<TMyVertex*> global_vertex_list;
t_my_polygon.Add_Vertex(TRefVertex(TMyVertex(-1, -1, 0), global_vertex_list));
t_my_polygon.Add_Vertex(TRefVertex(TMyVertex( 1, -1, 0), global_vertex_list));
t_my_polygon.Add_Vertex(TRefVertex(TMyVertex( 1, 1, 0), global_vertex_list));
t_my_polygon.Add_Vertex(TRefVertex(TMyVertex(-1, 1, 0), global_vertex_list));
// add some vertices
Vector3f v_center = t_my_polygon.v_Center();
TRefVertex t_center(t_my_polygon.v_Center2(), global_vertex_list);
// get center position and center vertex
}
// test with global vertex list
return 0;
}
This code snippet creates quad, centered arround origin and calculates it's centre as a vector (position only) and as a vertex (including the other coordinates).
Now we could consider adding lots of useful functions, but i'm actually going to add normal plane calculation only and then we'll try to draw some polygons using OpenGL and we're done today.
Normal plane is analytic plane polygon lies on. It can be found as cross product of two non-colinear, non-zero vectors lying in the same plane as the polygon. It yields normal vector (or direction) which is perpendicular to normal plane. Analytical plane has one more parameter which can be determined as negative dot product of normal vector and one of polygon's vertex positions. It's quite simple to write, but it's necessary to be careful about non-colinearity and non-zero length of vectors as that can easily happen and then invalid normal vector is calculated (which can be quite destructive, for example for space subdivision algorithms. It would cause errors in lighting calculations as well) Here it is:
/*
* bool Calc_Normal()
* - calculate normal, return false if there wasn't trinity
* of vertices to construct plane from
* - it has to be called explicitly, it is never called by CPolygon2 itself
*/
bool Calc_Normal()
{
if(m_vertex_list.size() < 3)
return false;
// impossible with so little vertices
for(int i = 1; i < m_vertex_list.size(); ++ i) {
Vector3f v_u = (Vector3f)m_vertex_list[i - 1] - (Vector3f)m_vertex_list[i];
if(v_u.f_Length() < f_epsilon)
continue;
// get non-zero vector
for(int j = 0; j < m_vertex_list.size(); ++ j) {
if(j == i || j == i - 1)
continue;
Vector3f v_v = (Vector3f)m_vertex_list[j] - (Vector3f)m_vertex_list[i];
if(v_v.f_Length() < f_epsilon)
continue;
// get another different non-zero vector
Vector3f v_normal = v_u.v_Cross(v_v);
if(v_normal.f_Length() < f_epsilon)
continue;
v_normal.Normalize();
// colinear vectors would yield zero normal
m_t_normal = Plane3f(m_vertex_list[0], v_normal);
return true;
// create plane
}
}
return false;
}
/*
* inline const Plane3f &t_Normal() const
* - normal access function
*/
inline const Plane3f &t_Normal() const
{
return m_t_normal;
}
I guess there is quite a lot of code and too little talk and i apologise about that, because it doesn't give you very much space for thinking about your own sollutions. I hope it's going to change as more advanced topics kick in. Now for the final touch, rendering using OpenGL. For compatibility purposes i'm going to use GLUT as there's no problem compiling GLUT program on linux or windows either.
GLUT basics
GLUT is an utility library for OpenGL. It contains some handy functions, written in C. We're going to use it for OpenGL initialization and keyboyard / mouse response only. The main reason to use GLUT here is it's os independent (the same code is compilable under linux as well as under windows) I'd like to note this is by no means any GLUT reference, i'll just cover the very basics, you have to refer to GLUT specifications (available at OpenGL.org) for details.
GLUT works basically by registering callback functions, there is callback for every single action that is supported. We're going to use display callback which is responsible for redrawing contents of the screen and mouse motion, passive mouse motion and mouse click callbacks to respond to mouse events. (passive mouse motion is mouse motion when no button is held, whereby mouse motion basically happens when dragging something somewhere) No need for keyboyard so far. Here is a very simple piece of code, utilizing GLUT:
#ifdef WIN32
#include <windows.h> // gl.h needs some typedefs
#endif
#include <GL/gl.h>
#include <GL/glut.h>
float f_mouse_x, f_mouse_y;
// mouse cursor in OpenGL coordinates
int n_width = 640, n_height = 480;
// window size
// here we usualy draw glViewport and all commands
// to be called just once before drawing many frames
void onResize(int n_new_width, int n_new_height)
{
glViewport(0, 0, n_width = n_new_width, n_height = n_new_height);
// set new viewport
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
// set ortho projection
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
// set camera
glPointSize(4);
// set point size
glColor3f(1, 1, 1);
// white
}
// here we render frame
void onDisplay()
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glBegin(GL_LINES);
glVertex2f(-.5f, 0);
glVertex2f(.5f, 0);
glEnd();
// draw line
glBegin(GL_POINTS);
glVertex2f(f_mouse_x, f_mouse_y);
glEnd();
// draw cursor (note it redraws when dragging only)
glutSwapBuffers();
// display results
}
// here we receive notifications on mouse clicks
// x and y are cursor coordinates in pixels
void onMouseClick(int button, int state, int x, int y)
{
f_mouse_x = (2.0f * x) / n_width - 1;
f_mouse_y = 1 - (2.0f * y) / n_height;
// get current mouse position
switch(button) {
case GLUT_LEFT_BUTTON:
break;
case GLUT_RIGHT_BUTTON:
break;
case GLUT_MIDDLE_BUTTON:
break;
};
// in case button is going to be important for dragging, it's necessary to remember it
}
// here we receive notifications on mouse motion when dragging
// something, x and y are cursor coordinates in pixels
void onMouseMotion(int x, int y)
{
f_mouse_x = (2.0f * x) / n_width - 1;
f_mouse_y = 1 - (2.0f * y) / n_height;
// get current mouse position
glutPostRedisplay();
// asume we changed something and now we want to redraw ...
}
// here we receive notifications on mouse motion when just moving
// the mouse, x and y are cursor coordinates in pixels
void onPassiveMouseMotion(int x, int y)
{
f_mouse_x = (2.0f * x) / n_width - 1;
f_mouse_y = 1 - (2.0f * y) / n_height;
// get current mouse position
}
int main(int n_arg_num, const char **p_arg_list)
{
glutInit(&n_arg_num, (char **)p_arg_list); // init glut; it's possible to pass
// configuration / commands using commandline
glutInitDisplayMode(GLUT_RGBA | GLUT_DEPTH | GLUT_DOUBLE);
// RGBA framebuffer with Z-buffer and back-buffer for smooth frame flipping
glutInitWindowSize(n_width, n_height); // window size
glutCreateWindow("convex.madness"); // window title
// init OpenGL using GLUT
// now we could load textures and or do other initialization
//glutIdleFunc(onDisplay); // we could use this to constantly
// redraw image, but it's better to use glutPostRedisplay()
glutDisplayFunc(onDisplay);
glutReshapeFunc(onResize);
glutMouseFunc(onMouseClick);
glutMotionFunc(onMouseMotion);
glutPassiveMotionFunc(onPassiveMouseMotion);
// register our callbacks
glutMainLoop();
// begin rendering
return 0;
}
It's densely commented, you should have no problems understanding it when you read it. The only thing to notice is how i avoided repeatedly calling OpenGL commands in onDisplay() and moved them to onResize() function (which is called after window has been created and then when user resize window only, whereby onDisplay() is called much more frequently). In case you compile it with any C compiler, link it with glut ("-lglut -lopengl" under linux, "opengl32.lib glut32.lib" in msvc) you get black window showing white horizontal line and a dot you can drag using mouse. Note the dot actually moves with the mouse cursor all the time, but the window redraws when moving mouse while holding any of it's buttons only.
What we're going to need for couple of first issues is capability to draw a polygon and maybe move it's vertices. Both can be easily fixed using C++. I've added member function called for_each_vertex() to our polygon class. It's behavior is essentialy the same as std::for_each() so it's easy to write small function object for passing vertices to OpenGL:
/*
* class CDrawPolygon
* - simple function object we can use to simply pass polygon's vertices to OpenGL
*/
class CDrawPolygon {
public:
inline void operator ()(const TRefVertex<TMyVertex> &r_t_vertex) const
{
TMyVertex *p_ref = r_t_vertex.m_p_ref;
for(int i = 0; i < 4; ++ i) {
glMultiTexCoord4f(GL_TEXTURE0 + i, p_ref->p_texcoord[i].x,
p_ref->p_texcoord[i].y, p_ref->p_texcoord[i].z, p_ref->p_texcoord[i].w);
}
glColor4f(p_ref->v_color.x, p_ref->v_color.y, p_ref->v_color.z, p_ref->v_color.w);
glNormal3f(p_ref->v_normal.x, p_ref->v_normal.y, p_ref->v_normal.z);
glVertex3f(p_ref->v_position.x, p_ref->v_position.y, p_ref->v_position.z);
}
};
void onDisplay(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glBegin(GL_POLYGON);
my_polygon.for_each_vertex(CDrawPolygon());
glEnd();
// easily draw polygon
// ... some more code
glutSwapBuffers();
}
The same goes for selecting vertices by mouse. On mouse click we run trough vertex list and find some vertex that is close enough to cursor. Remember it's pointer or reference and then just change it's coordinates when dragging mouse. Should be really simple for you to imagine what is going on now so i'm not going to put here the code. You're going to see it in the next issues.
Two final notes on drawing. One - we won't need to specify all the vertex coordinates, just position will do for the couple of first examples. Two - this would be too slow for drawing bigger amounts of polygons. It's not because vertex data are in vector which is referenced from another vector inside polygon, we've done everything for compiller to make it easy to inline most of stuff so verry little assembly instructions are emitted, but calling "small" OpenGL commands again and again isn't a good practise. The sollution is right here ...
Using vertex arrays and vertex buffer objects
We will create vertex array as it's supported on most todays graphics cards or vertex buffer object which is much faster because vertex data are in fast graphics card memory but is not so well supported (it's generally supported nowadays, but there are always some people with ancient machines) Then we can draw all the geometry with just a few (like 6) OpenGL commands.
I'm going to use part of ÜberLame framework, namely OpenGL extension handler and CVertexBufferObject class. I've included those files inside todays code packet so it's more convenient to compile.
When creating vertex arrays in OpenGL, one can create either interleaved array which is in fact array of vertex structures (there is several pre-defined formats which can be used) or several separate arrays, one for every vertex component (array with positions, array with normals, with colors, etc ...) Performance is the same (on earlier cards interleaved arrays might have been faster because data went in order it was needed by the pipeline, unlike with separate arrays it's necessary to read from several different parts of memory) We could stick to simple interleaved array today as it's a bit simpler.
Next we need bunch of small index arrays, one per each polygon (in reality it will be one big index array which we will be referencing with some offset) It's a bit better to use triangle strips instead of polygons as they don't need to be convex nor planar and therefore can contain more geometry (and so reduce number of OpenGL calls necessary to draw the frame)
When we have both those arrays ready (which we don't - yet), we either give OpenGL the pointers and start drawing right away or copy arrays to vertex buffer objects (once, not every frame) and then start drawing. The following code can be used to get raw vertex and index arrays from vector of polygons:
class CVertexArrays {
protected:
unsigned int n_vertex_num;
unsigned int n_vertex_size;
GLenum n_vertex_format;
float *p_vertex_array; // vertex coordinates
unsigned int n_index_num;
unsigned int *p_index_array; // vertex indices for all polygons
unsigned int n_polygon_num;
GLsizei *p_vertex_count; // vertex count for every polygon
unsigned int **p_vertex_pointer; // pointer to first vertex index
// in p_index_array for every polygon
// a few function object classes
public:
/*
* CVertexArrays(std::vector<CPolygon2<TRefVertex> >::const_iterator p_begin,
* std::vector<CPolygon2<TRefVertex> >::const_iterator p_end,
* const std::vector<TMyVertex*> &r_global_vertex_list)
* - default constructor
* - p_begin and p_end are two iterators from list of polygons, delimiting
* first and last polygon to be added to the array
* - r_global_vertex_list is reference to global vertex list
* (coordinates will be taken out of there)
*/
CVertexArrays(std::vector<CPolygon2<TRefVertex> >::const_iterator p_begin,
std::vector<CPolygon2<TRefVertex> >::const_iterator p_end,
const std::vector<TMyVertex*> &r_global_vertex_list);
/*
* ~CVertexArrays()
* - default destructor
*/
~CVertexArrays();
/*
* bool b_Ready() const
* - returns true in case constructor succeeded in creating
* all the neccesary arrays, otherwise returns false
*/
bool b_Ready() const;
/*
* void Render() const
* - render geometry using vertex arrays
*/
void Render() const
{
glEnableClientState(GL_VERTEX_ARRAY);
glEnableClientState(GL_NORMAL_ARRAY);
// those things will be taken from vertex array
// instead of glVertex3f / glNormal3f
glInterleavedArrays(n_vertex_format, n_vertex_size * sizeof(float), p_vertex_array);
// give OpenGL pointer to our vertices
glMultiDrawElements(GL_POLYGON, p_vertex_count,
GL_UNSIGNED_INT, (const void**)p_vertex_pointer, n_polygon_num);
// draw all the polygons using a single call
glDisableClientState(GL_VERTEX_ARRAY);
glDisableClientState(GL_NORMAL_ARRAY);
}
};
It's very simple class which transforms list of polygons into a few arrays with vertex coordinates and indices so it's possible to draw it using OpenGL.
As you can see in Render() function, we still have vertices in system memory, we pass pointer to it only. I promised vertex buffer objects which will not complicate things very much, because it's just necessary to create buffer for vertices, copy them inside and then tell OpenGL to source vertices from there. That's all it's needed to be done to use vertex buffer objects. Note glMultiDrawElements() function is available since OpenGL1.4 so it won't run on older cards.
Note in case vertex buffer is bound, all functions expecting vertex index pointer interpret the pointer passed to them as offset in the buffer. If it's necessary to pass pointer to the beginning of the buffer (which is our case) zero pointer will be used! The same goes for indices. It's pointed out in comments in demo source code.
Adding a few more lines of code we've seen already, it's possible to create glut window and draw something. We've created a single quad when we tested if our polygon class is capable of finding it's centre. It's not very catchy, watching it rotate though ... So i included header file, containing vertices for a simple model imported from 3DS MAX. (and i though rotating potatoes were over the hill, lol)
Convex madness demo 01
Conclusion
So, a little recap about what it does and what it doesn't do. It contains very simple polygon template, two vertex classes that can be used as template parameters, there is class for packing data from polygons to vertex arrays and drawing them. Then there's a bunch of simplified ÜberLame files, containing OpenGL extension handler,
Now it creates bunch of polygons from static data, converts them to vertex array and draw it. In the future more common use case would be loading some data, then performing some operations with polygons then displaying the results. We won't be always able to use vertex arrays as they are static so in case we will offen change polygon topologies or vertex coordinates, we will have to rely on calling old faithful glVertex() as that is the simplest way and should be fast enough for our purposes.
